计量经济学是一门结合经济理论、数学和统计学的学科,旨在通过构建模型来分析经济现象,并揭示变量之间的定量关系。在这一领域中,模型的构建是核心任务之一。本文将探讨计量经济学中六种主要模型的含义及其应用,帮助读者深入理解这一重要工具的功能和意义。
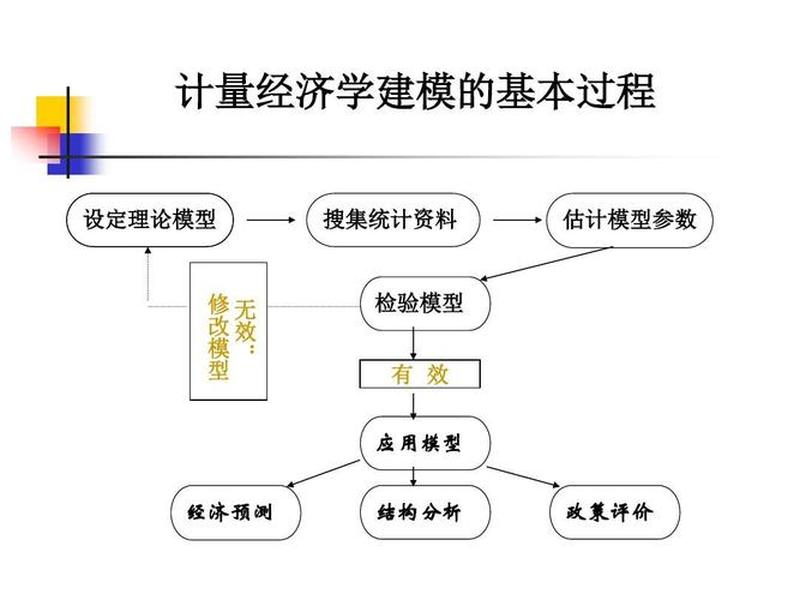
计量经济学模型的基本概念
计量经济学模型通常由一个或多个随机方程组成,这些方程简洁而有效地描述了真实经济系统的数量特征。模型通过变量和系数的组合,揭示了经济活动中各个因素之间的定量关系。建立模型的之一步是确定研究对象及其相关变量。这些变量分为被解释变量和解释变量,其中被解释变量是研究的主要目标,而解释变量则是影响被解释变量的因素。
线性回归模型
线性回归模型是计量经济学中最常用的一种模型,主要用于描述因变量与一个或多个自变量之间的线性关系。在这一模型中,假设因变量与自变量之间存在线性关系,即可以用一个线性方程来表示。通过最小二乘法等技术,可以估计出模型中的参数,从而进行预测和分析。线性回归模型适用于许多实际问题,如消费行为、生产函数等,但其假设条件(如误差项独立同分布)需要得到满足。
多元回归模型
多元回归模型是对线性回归模型的扩展,它允许同时考虑多个自变量对因变量的影响。这种模型在实际应用中非常普遍,因为经济现象往往受到多个因素的影响。通过多元回归分析,研究者可以识别出各个自变量对因变量的重要性,并进行相应的政策建议。多元回归模型也面临着多重共线性的问题,即自变量之间可能存在高度相关性,这会影响参数估计的稳定性。
时间序列模型
时间序列模型用于分析随时间变化的数据。这类模型考虑了数据中的时间依赖性,常用于经济预测和政策评估。ARIMA(自回归积分滑动平均)模型是时间序列分析中的经典 xxx ,它通过历史数据来预测未来趋势。季节性调整也是时间序列分析中的重要步骤,以消除季节波动对数据分析的影响。
面板数据模型
面板数据模型结合了时间序列数据和截面数据,能够提供更丰富的信息。这种模型允许研究者在多个个体(如公司或国家)上观察同一现象随时间变化的情况。通过使用固定效应或随机效应 xxx ,面板数据模型能够有效控制未观测到的异质性,提高估计结果的准确性。这使得面板数据模型在政策评估和跨国比较研究中得到了广泛应用。
结构方程模型
结构方程模型是一种复杂但强大的统计工具,用于分析多个因果关系。它允许研究者同时估计多个方程,并评估潜在变量之间的关系。这种 xxx 特别适合于社会科学领域,因为许多社会现象往往涉及到隐含因素,如心理因素、社会规范等。结构方程模型不仅能够验证理论假设,还可以提供更深入的因果推断。
非参数与半参数模型
非参数与半参数模型不依赖于特定的分布假设,因此在处理复杂或未知形式的数据时非常有效。这些模型允许更大的灵活性,可以捕捉到数据中的非线性关系。非参数 xxx 通常使用核密度估计等技术,而半参数 xxx 则结合了参数和非参数特征,在保持一定结构假设的允许部分自由度。
相关内容的知识扩展:
理论与实践结合的重要性不可忽视。在建立计量经济学模型时,理论框架提供了必要的指导,而实践中的数据则为理论提供了实证支持。在进行任何计量经济学研究时,必须确保理论基础与实际数据相结合,以提高研究结果的可靠性。
数据质量对结果影响深远。在计量经济学中,数据不仅要具有代表性,还需具备准确性和一致性。高质量的数据能够显著提高模型估计的精度,而低质量的数据则可能导致错误结论。研究者在选择和处理数据时,应特别关注其来源和处理过程,以确保最终结果能够真实反映经济现象。
技术进步推动计量经济学的发展。随着计算机技术和统计软件的发展,复杂计算变得更加可行,使得更多高级计量经济学 xxx 得以应用。例如,大数据技术使得处理海量信息成为可能,从而推动了新型计量经济学 xxx 的发展。这一趋势不仅提高了研究效率,也为政策制定提供了更为科学的数据支持。
计量经济学中的六种主要模型各具特色,各自在不同领域发挥着重要作用。通过深入理解这些模型及其应用背景,可以更好地利用计量经济学工具进行经济分析与决策支持。